ÁREA DO ALUNO
ACESSE LINKS EXPLICATIVOS
EM TODO O TEXTO ESCRITO EM AZUL.
-> Continuaremos com o estudo dos limites das funções que envolvem quocientes de polinômios em uma indeterminação do tipo  , porém com o “agravante” da raiz quadrada. A resolução deste tipo de limite envolve a multiplicação pelo o que chamaremos de conjugado.
, porém com o “agravante” da raiz quadrada. A resolução deste tipo de limite envolve a multiplicação pelo o que chamaremos de conjugado.
Exemplo_2.2 -
a) Verifique o comportamento da 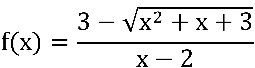 com
com 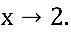
Simbolicamente, calcule:
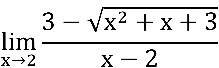
Temos uma indeterminação do tipo  , pois
, pois
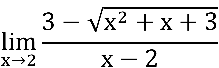
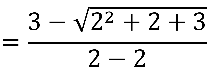
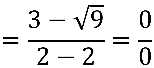
Para resolver o "problema" buscaremos uma função equivalente através da multiplicação pelo conjugado do numerador. O numerador pode ser visualizado como:
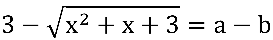
, sendo 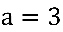 e
e 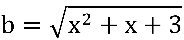 .
.
O conjugado de a-b é a+b, e vice-versa. Neste caso:
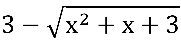 tem como conjugado:
tem como conjugado: 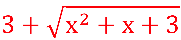
Quando multiplicamos:
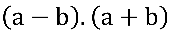
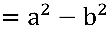
, temos uma diferença de dois quadrados.
A multiplicação pelo conjugado tem como objetivo a “eliminação” da raiz quadrada que é o agravante inicial neste problema.
Multiplicando e dividindo a função inicial pelo conjugado do numerador, temos:
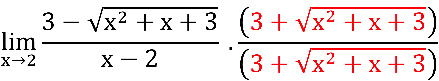
Observação: devemos multiplicar e dividir pelo conjugado para não alterarmos a expressão!
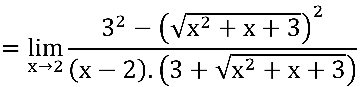
A princípio este função equivalente é mais assustadora que a original, porém, como veremos, a indeterminação inicial que envolvia a raiz quadrada não aparece nesta função.
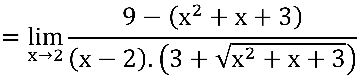
, neste passo a raiz quadrada do numerador foi “eliminada” visto que:
.png)
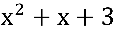
, fazendo a multiplicação por -1 :
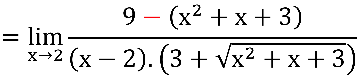
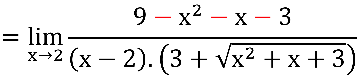
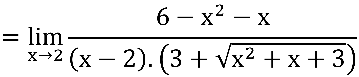
Vale notar que, com a multiplicação e divisão pelo conjugado, inserimos uma raiz quadrada no denominador. Porém, esta raiz, que é parte do conjugado, não é um problema porque se  o conjugado
o conjugado  .
.
Apesar da eliminação da raiz quadrada do numerador ainda temos uma indeterminação  .
.
.png)
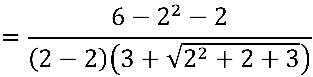
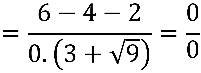
Porém o problema não envolve mais a raiz quadrada e sim o quociente descrito em verde:
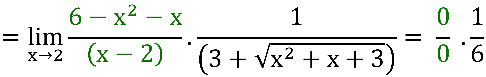
o que nos leva a um problema do tipo estudado no capitulo anterior.
Fazendo a fatoração algébrica do numerador.
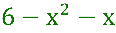
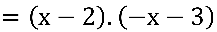
ficamos com:
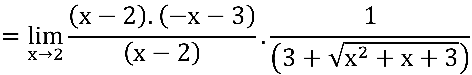
, simplificando:
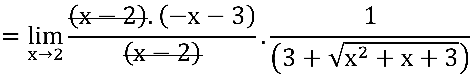
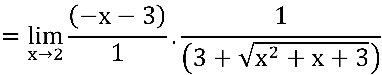
.png)
Concluímos que:

Visualize o resultado abaixo.
.png)
Fig_2-2-a – Gráfico da função 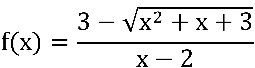 .
.
b) Verifique o comportamento da função 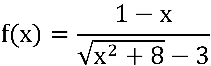 com
com 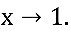
Simbolicamente, calcule:
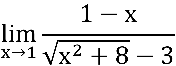
Temos uma indeterminação do tipo  , pois
, pois
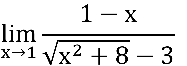
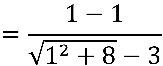
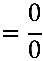
O denominador pode ser visualizado como:
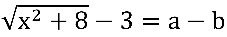
, sendo 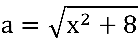 e
e 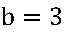 .
.
Neste caso: 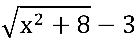 tem como conjugado:
tem como conjugado: 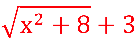
Multiplicando e dividindo pelo conjugado:
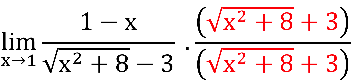
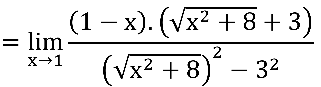
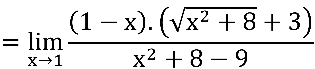
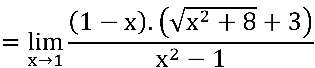
Notem que ainda temos indeterminação 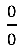 no quociente em verde:
no quociente em verde:
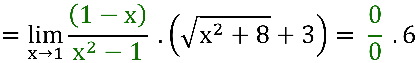
, usando a diferença de dois quadrados no denominador em verde:
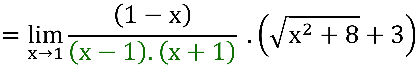
, o quociente em amarelo na expressão abaixo resulta em -1.
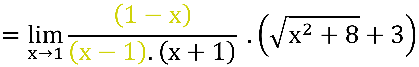
Observe:

Ficamos com:
.png)
Concluimos que:
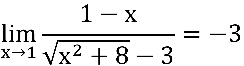
Visualize o resultado abaixo.
.png)
Fig_2-2-b – Gráfico da função 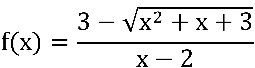 .
.
c) Verifique o comportamento da função 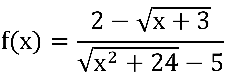 com
com 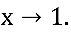
Simbolicamente, calcule:
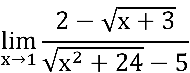
Temos uma indeterminação do tipo  , pois
, pois
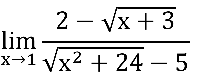
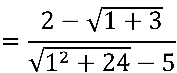
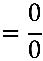
Neste caso temos um “problema duplo”, devemos utilizar o método do conjugado para “eliminar” a raiz quadrada do denominador e a do numerador. Inicialmente multiplicamos e dividimos pelo conjugado do numerador:
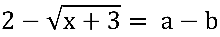
, sendo 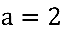 e
e 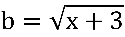 .
.
Neste caso: 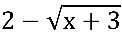 tem como conjugado:
tem como conjugado: 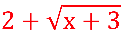 .
.
Multiplicando e dividindo pelo conjugado do numerador:
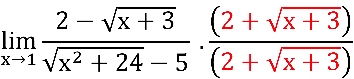
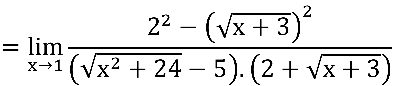
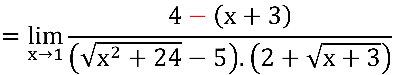

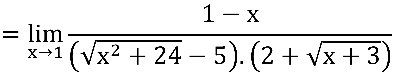
Notem que ainda temos indeterminação 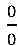 no quociente em verde:
no quociente em verde:
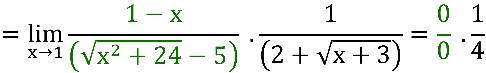
O conjugado do denominador:
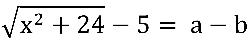
, sendo 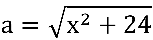 e
e 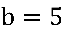 .
.
Neste caso: .png) tem como conjugado:
tem como conjugado:.png)
Multiplicando e dividindo pelo conjugado do denominador:
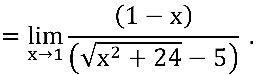
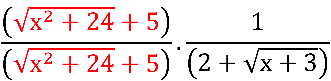
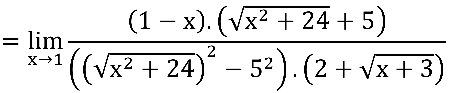
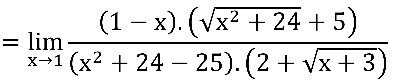
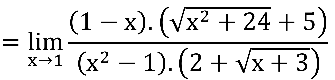
Notem que ainda temos indeterminação 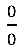 no quociente em verde:
no quociente em verde:
.png)
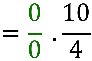
, usando a diferença de dois quadrados no denominador em verde:
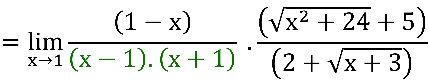
, o quociente em amarelo na expressão abaixo resulta em -1.
.png)
.png)
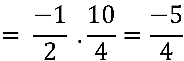
Concluimos que:
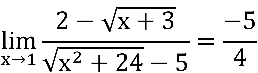
Visualize o resultado abaixo.
.png)
Fig_2-2-c – Gráfico da função 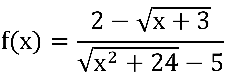 .
.
d) Verifique o comportamento da função 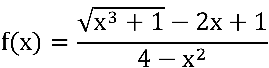 com
com 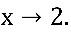
Simbolicamente, calcule:
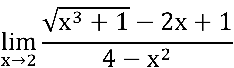
Temos uma indeterminação do tipo  , pois
, pois
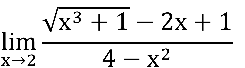
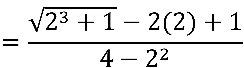
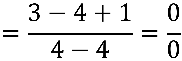
Para identificarmos o conjugado do numerador, inicialmente, reescreveremos o numerador como:
.png)
Reescrevendo o limite original:
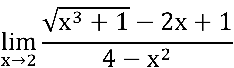
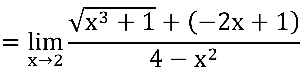
Neste formato fica evidente que:
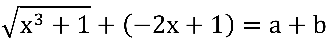
sendo: 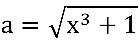 e
e 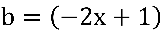 .
.
Neste caso: 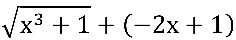 tem comoconjugado:
tem comoconjugado:  .
.
Multiplicando e dividindo pelo conjugado do numerador:
.png)
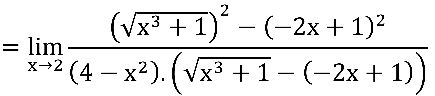
, observe que:
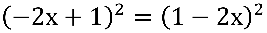
que é uma diferença ao quadrado :

, portanto:
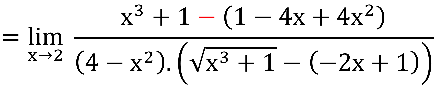
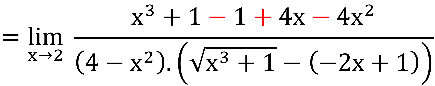
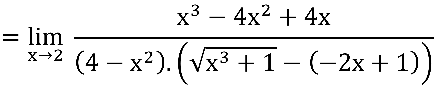
Notem que ainda temos indeterminação 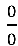 no quociente em verde:
no quociente em verde:
.png)
, usando a fatoração algébrica no numerador e no denominador em verde:
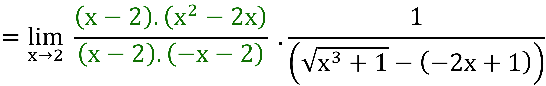
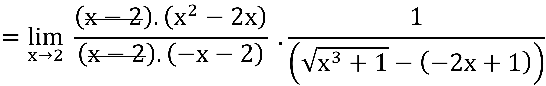
.png)
Concluimos que:
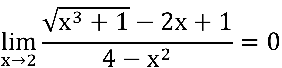
Visualize o resultado abaixo.
.png)
Fig_2-2-d – Gráfico da função 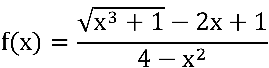 .
.
© 2025 - Todos os direitos reservados a Portal Optimum by Agencia Giga